東大ぱふぇっとです。
世の中には算術平均と幾何平均というものが存在します。
株式投資の利回りを計算する際には幾何平均を用いる必要があります。
このブログでは難解な用語は極力用いないのですが、今回は敢えて難解な用語を用いています。
幾何平均とは聞き慣れない言葉かもしれません。
でも大丈夫。
誰でも分かるように簡単な言葉でしっかりと解説していきます🐰
平均には色々な種類がある
実は平均にはいろいろな種類があるのです。
『平均にはいろいろな種類がある』って言われると「マジか！？」ってなる人もいるかもしれませんが、株クラなら誰もが耳にしたことのある『平均』も存在します。
それは時価総額加重平均ですね。
一度は聞いたことがあるでしょう。そう、平均にはいろいろな種類があるのです。
算術平均と幾何平均とは？
算術平均と幾何平均って言われるとちょっと怖いかもしれませんが、算術平均とは足し算の平均を表します。
平均身長とか平均体重とかは算術平均ですね。一般的に言われる平均は算術平均を示します。
幾何平均とは掛け算の平均を表します。
『年利平均7％』というのは毎年のリターンを掛け算していって平均にしたら7％になったということですので、これは幾何平均ですね。
- 算術平均→一般的によく使われる平均。足し算の平均。
例）平均身長・平均体重 - 幾何平均→日常生活ではあまり使わない。掛け算の平均。
例）年間平均リターン7%
1年目は年利30%、2年目は年利10％、平均リターンはどうなるでしょう？
| 1年目 | 30％ |
| 2年目 | 10％ |
| 平均 | ？？？ |
こう聞かれると直感的には年利20％っぽく見えてしまいますが、実際の計算方法は1.3*1.1をしたあとにルートをつける感じですね。
仮に平均リターンが年利20%とすると…
- 1.2*1.2（平均リターン（？）を掛け算）
- 1.3*1.1（毎年のリターンを掛け算）
この両者の値が等しくなるはずですが、当然ながらこれらの値は異なりますね。さりげなく背理法を使っていますが背理法は中学数学の範囲内なのでセーフですね。ルートの計算結果をブログに書くのは面倒なのです。
この時点で間違えているインフルエンサーがいたりしますので…気をつけましょう。
って数ヶ月前の記事に書いていたんですが、最近も間違えているインフルエンサーがいましたね。
インフルエンサーは影響力は高いですが中身が伴っているとは限りません。
算数ができるとは限りません。日本語が読めるとは限りません。
情報の真偽やインフルエンサーの投資レベルについてはあなた自身が判断する必要があります。
当然ながら東大ぱふぇっとが言っていることが合っているか間違っているかもあなた自身が判断してくださいね🐰
算術平均の求め方！
算術平均とは
足し算の平均のことです。
平均体重、平均身長、
色々使われていますね。
ここで、算術平均を求める公式を
確認しておきましょう。
算術平均＝足し算の合計÷個数
個数で割るのがポイントですね！
小学校5年生で
習った内容です。
忘れがちなので
気をつけましょう！
個数で割り算をしよう！
ここからは算数ではなく数学のお話になります。
算術平均と幾何平均の違い！
図解、本当にいる…？
…いるかぁ…。
ご存知のかたもいらっしゃるかと思いますが、私は結構かなりめんどくさがり屋さんなのです。
算術平均と幾何平均の違いを図解！
本当に面倒くさいんですが、図を作りました。
1年目のリターンを右方向、2年目のリターンを下方向に表現します。
各年のリターンは以下の感じでいきます。
| 1年目 | 30％ |
| 2年目 | 10％ |
| 平均 | ？？？ |
初期状態
初期状態では面積100ですね。
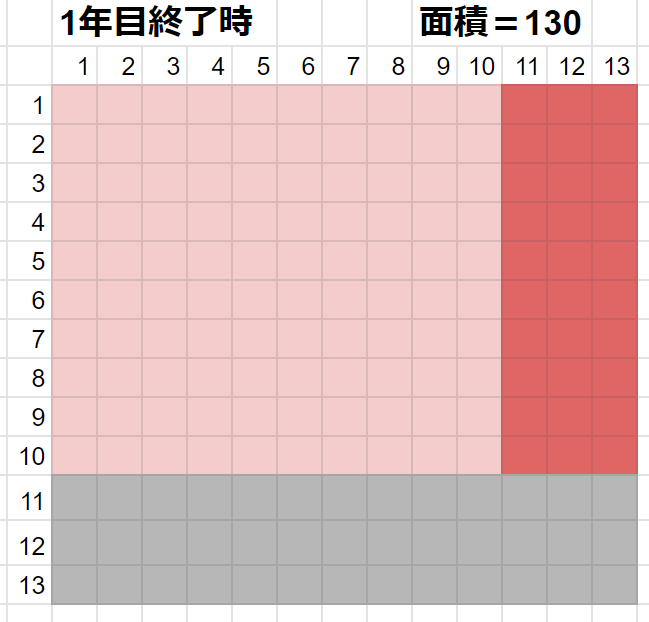
1年目終了時
30%増えました。右方向に3マス延ばしました。面積130ですね。
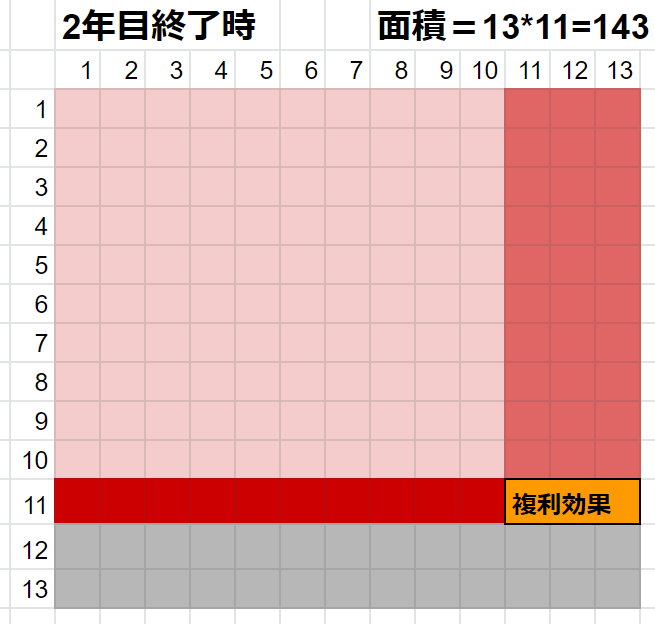
2年目終了時
10%増えました。下方向に1マス延ばしました。面積143ですね。
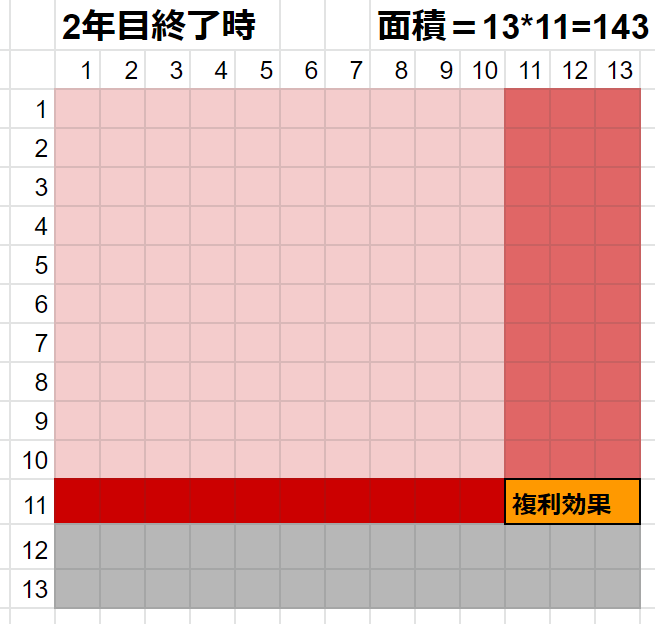
余談ですがオレンジの3マスは複利効果によるものですね。
マス目の計算には掛け算を使っていますよね。縦×横です。
このように毎年のリターンは掛け算で増えていきます。
掛け算で増えていくからこそ、複利効果が生まれるのです。
掛け算の平均とは何を意味するか？
掛け算の平均とは何を意味するのか、もう一度考えてみましょう。
先の説明をちょっと再掲します。
仮に平均リターンが年利20%とすると…
- 1.2*1.2（平均リターン（？）を掛け算）
- 1.3*1.1（毎年のリターンを掛け算）
この両者の値が等しくなるはずですが、当然ながらこれらの値は異なりますね。よって算術平均と幾何平均は上記の例では異なることが分かります。
逆に言えば、
- 1.3*1.1（毎年のリターンを掛け算）
と同じになる値を求めれば良いのです。掛け算の答えが一致すれば良いわけですね。
掛け算の答えを一致させる！
掛け算の答えを一致させれば良い。
これはつまり面積が一緒であれば良いわけですね。
そして平均値を求めるのですから、同じ値を掛け算するわけです。
平均年利5%って言われたら、1.05を2回掛け算しますよね？同じ値を掛け算するわけです。1.2*1.2みたいに。
条件は2つでしたね。
- 面積が一致する
- 同じ値を掛け算する
同じ値を掛け算するのですから、縦と横の長さを一致させれば良いわけです。
つまり正方形です。
平均リターン7%！といった感じのが幾何平均でしたね。
幾何平均とは長方形の面積を変えずに正方形にする処理のことだったのです。
わかりやすい図解
Before
After
とろみづけ不要で簡単！馴染ませる必要はありません！
著作権への配慮
※本記事はクックドゥの○宝菜の販売促進活動を行っております。そのために商品画像を拝借いたしました。他の意図は一切ございません。
幾何平均の求め方！
ルートを付けます。終わり。算数ではなく数学です。
143にルートを付けます。
約11.96ですね。つまり1辺が約11.96の正方形は11*13の長方形と面積が一致するというわけですね。
図で示すと以下のようになります。
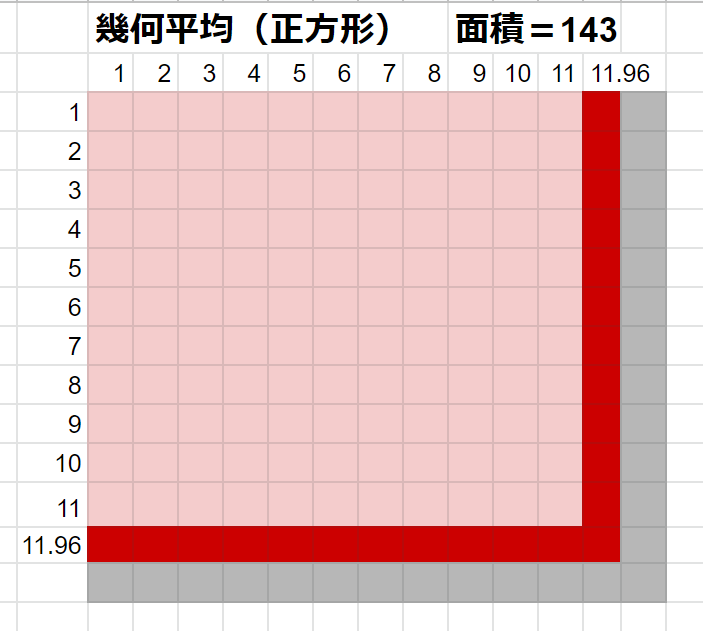
赤いマスは若干小さいので、面積は144ではなく143です！！！
足し算の平均は何を意味するか？
平均リターンを求める際に足し算の平均を求める人もいますよね。
（11+13）/2
みたいなやつですね。割り算を忘れる人もいるらしいですが、株式投資より自己投資したほうが良いですね。これは決して煽りではなく親身なアドバイスです。
さて、上の式は何を意味するのでしょうか？
図を見れば一目瞭然ですね。
掛け算、つまり面積について考えているのに、縦と横の長さの平均を求めているわけです。
縦と横の長さを足して2で割っているんですよ。おかしいですよね。
幾何平均とは長方形の面積を変えずに正方形にする処理のことです。掛け算の平均値ですね。
| 1年目 | 30％ |
| 2年目 | 10％ |
| 平均（？） | 20% |
これは間違いですね。
| 1年目 | 30％ |
| 2年目 | 10％ |
| 平均 | 約19.6% |
このようになりますね。平均は20%ではなく、約19.6％です。
10%アップ→1.1を掛ける。一辺の長さは11。
30%アップ→1.3を掛ける。一辺の長さは13。
よって、
一辺の長さが11.96→1.196を掛ける。19.6％アップですね。
※1辺10マスで示してるので百分率で表現するには10倍する必要があります。百分率とは％のことです。
ちゃんと合っていますね。
※小数点以下を適当に四捨五入したので、わずかに誤差が出ています。
・・・。
参考：平均リターンの求め方
なお、一般にルートの計算は手計算では面倒です。
今回は2年間の平均を求めたのでルートで済みましたが、n年間の平均リターンを求めるにはn個の掛け算の平均の計算が必要です。これはSpreadsheetを使うと良いでしょう。
例えば以下の数値設定を用いてみましょう。
＋8%の年
＋2%の年
±0%の年
ｰ5%の年
-10%の年
＋10%の年
掛け算の平均を求めるには、
=GEOMEAN()
という関数を用います。
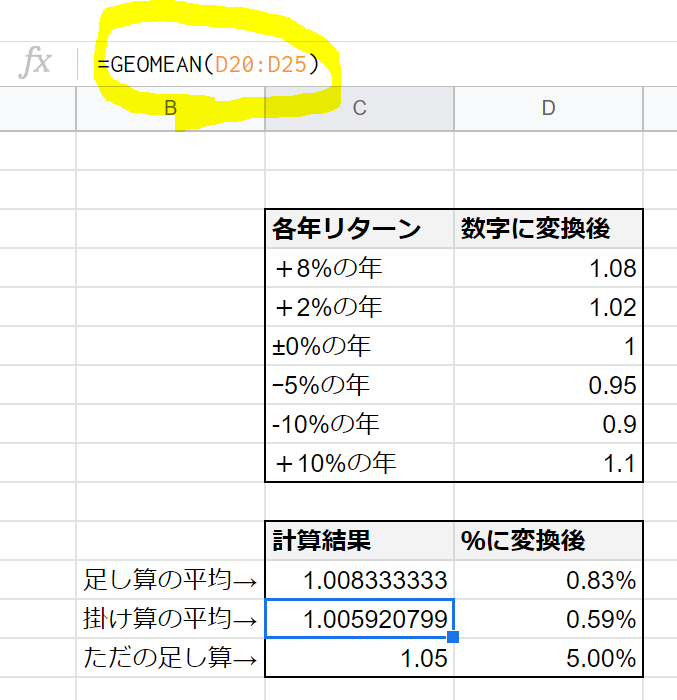
実際に計算してみました。
足し算の平均（）は0.83％ですね。ちなみにこの数値に何の意味もありません。
掛け算の平均は0.59％ですね。平均リターンは0.59％です。
ちなみにタダの足し算をしてみました。ピッタリと5%になりましたね。割り算を忘れるとこうなります。
ちなみにこの数字は6年間放置していたら初年度と比較して＋5%になったことを示す…と思いきや、毎年のリターンを掛け算しないといけないのに単純に足し算しているだけなので何の意味もありません。
足し算と掛け算の違いが分かっていない人が『複利は大切』などと言っているのは滑稽だと言わざるを得ません。足し算は単利でしょ。
まとめ
- 算術平均と幾何平均は大きく異なる。
- 算術平均は平均身長や平均体重など一般的に用いる平均。足したあとに個数で割り算しよう！
- 幾何平均は掛け算の平均。年間平均リターンを求めるときはこっち。
- 幾何平均とは図形的には長方形の面積を変えずに正方形にする処理。
- クックドゥを使うと料理が簡単で馴染ませる必要はない。
算術平均と幾何平均の違いを非常に分かりやすく説明した自信があります。いかがだったでしょうか。
インフルエンサーは影響力は高いですが中身が伴っているとは限りません。
算数ができるとは限りません。日本語が読めるとは限りません。
情報の真偽やインフルエンサーの頭脳レベルについてはあなた自身が判断する必要があります。
当然ながら東大ぱふぇっとが言っていることが合っているか間違っているかもあなた自身が判断してくださいね🐰
なお私は指数にレバレッジを掛けたら良いと考えています。
個別株で指数へのアウトパフォームは難しいなどと言われますが、指数に低レバレッジを掛けたら簡単にアウトパフォーム出来るじゃないですか。言っていることが合っているか間違っているかどうかはあなた自身が判断してくださいね🐰
同じ思想にたどり着いた方は、ようこそ。デリバティブ・インデックス投資の世界へ。
何か根に持ってるとか勘違いされたので一応追記しておきますが、特定の誰かに向けた記事ではないですね。算術平均と幾何平均の違いを理解しないまま、単利と複利の違いを理解しないまま、年間平均リターンを誤解したままFIREしてしまう被害者を少しでも減らすためにこの記事を書きました。
そもそも、算数わからない人に全く興味がないので申し訳ないけど根に持つとか以前の問題ですね…。
復習用おまけ
相場予測noteを無料お試しできるキャンペーン！
- 相場当てまくりの相場予測noteを無料で読める！
- 秘密の爆益銘柄を無料でチェックできる！
- 紙書籍が郵送されてくる！
- 総額1万円相当を無料でプレゼント！
超豪華な特別キャンペーンをIG証券様が実現してくれました！
- 私の相場予測を無料で読める！
- 総額1万円相当のプレゼントを無料でゲットできる！
IG証券でしか取り扱っていない投資対象が山ほど存在するため、私のように幅広い投資対象へ投資するなら必須の口座ですね！私自身もIG証券を利用しています！
秘密の爆益銘柄も公開中！
ブログの記事は全て無料で読めますが、相場予測noteに関しては有料記事となっています。
予言書とか言われちゃうレベル！？
驚異の的中率！爆益銘柄の公開！
別格すぎる相場予測を公開中！
☆相場予測note☆
モモの株式投資
やすチャンネル
バンガードS&P500ETF(VOO)に投資するりんりのブログ
